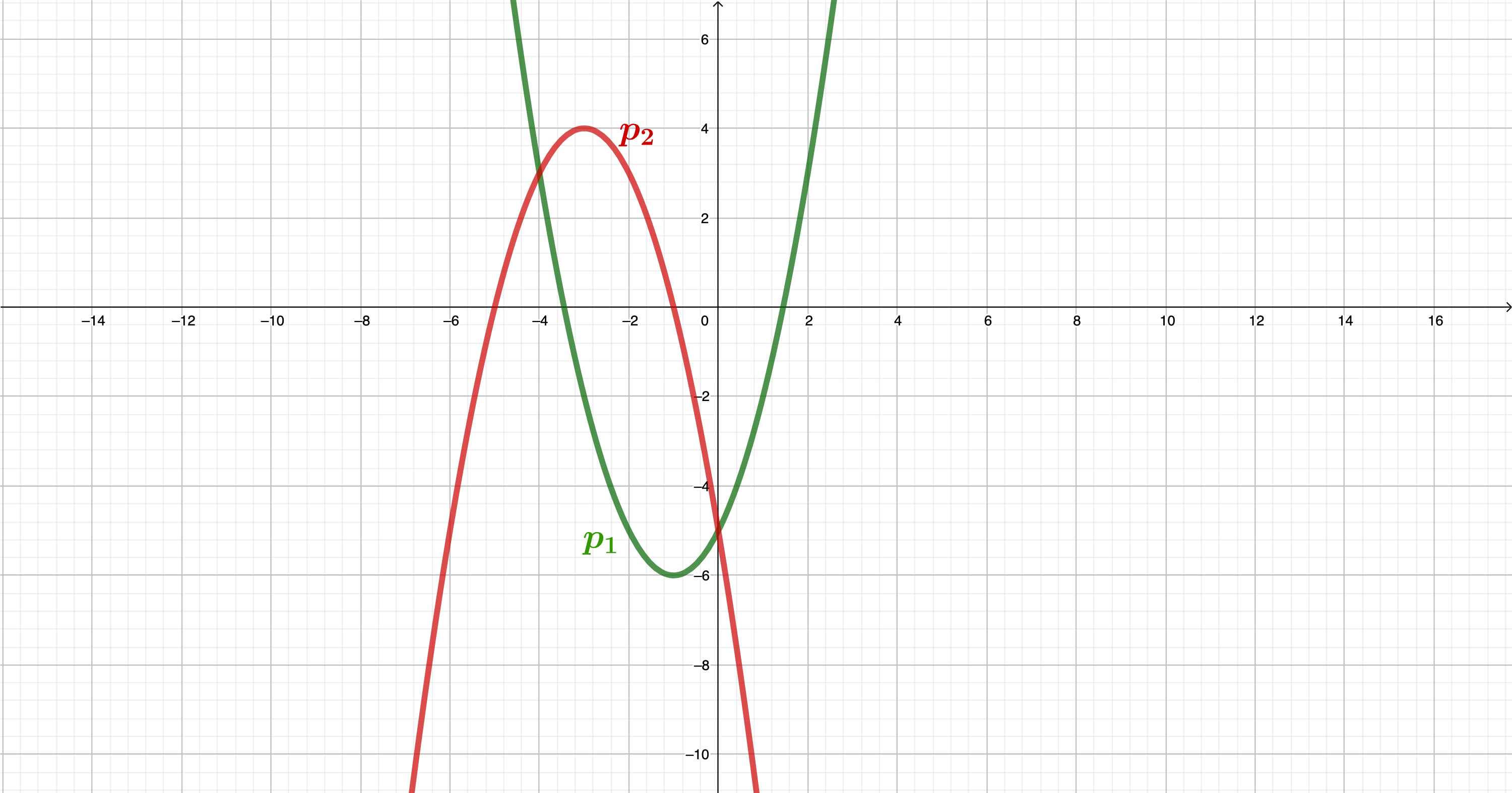
Lösen Sie die folgenden Aufgaben.
Die nach oben geöffnete Normalparabel hat den Scheitelpunkt
. Ermitteln Sie die Funktionsgleichung von in der Normalform.
Die Normalparabel hat die Funktionsgleichung : und schneidet die x-Achse in den Punkten und . Berechnen Sie die x-Koordinaten dieser Nullstellen.
Bestimmen Sie rechnerisch die Koordinaten des Scheitelpunkts der Normalparabel und geben Sie diesen an.
Zeichnen Sie die Parabeln und in ein Koordinatensystem mit der Längeneinheit 1 cm.
Eine nach oben geöffnete Normalparabel verläuft durch die Punkte und . Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Die Parabel hat die Funktionsgleichung : . Begründen Sie mithilfe einer Rechnung, dass die Parabel nach unten geöffnet ist.